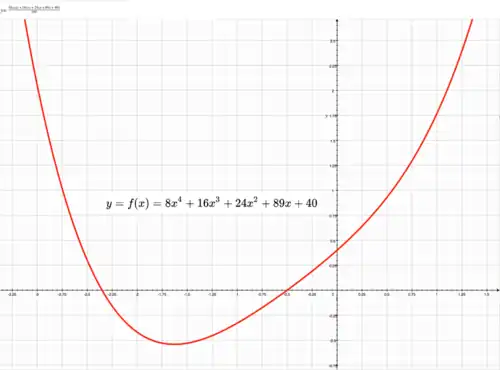
Quartic function
The quartic function is the bridge between the cubic function and more advanced functions such as the quintic and sextic.
Objective

|
Lesson
IntroductionThe quartic function is the sum of powers of from through :
usually written as:
If the function becomes Within this page we'll say that:
The quartic equation is the quartic function equated to zero: . Roots of the function are values of that satisfy the quartic equation.
Function as product of linear function and cubic
Function defined by 5 points
Function defined by 3 points and 2 slopes
Examples
|
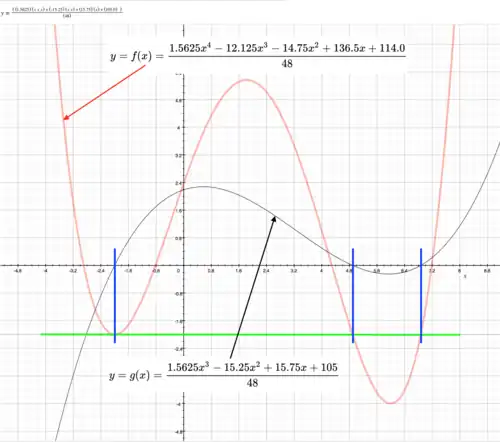
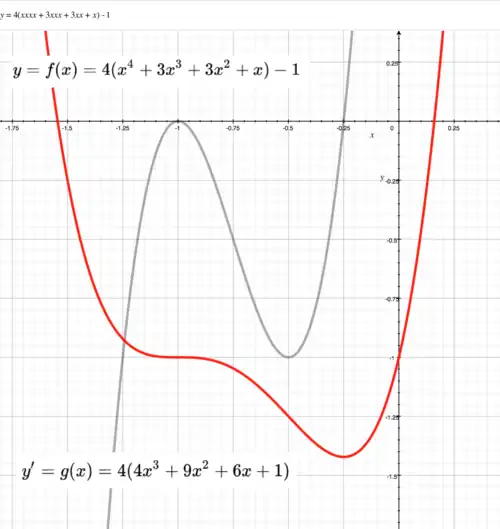
First and second derivatives
Points of inflection
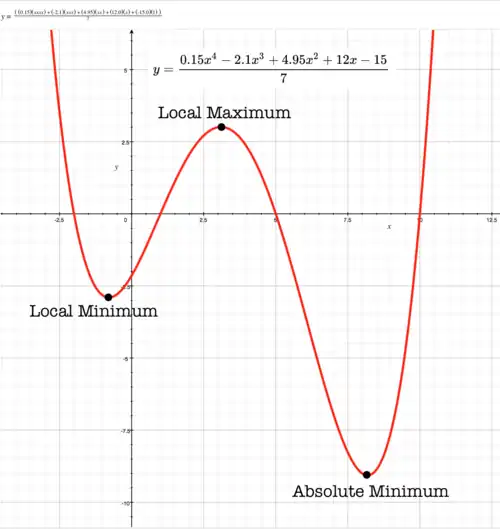
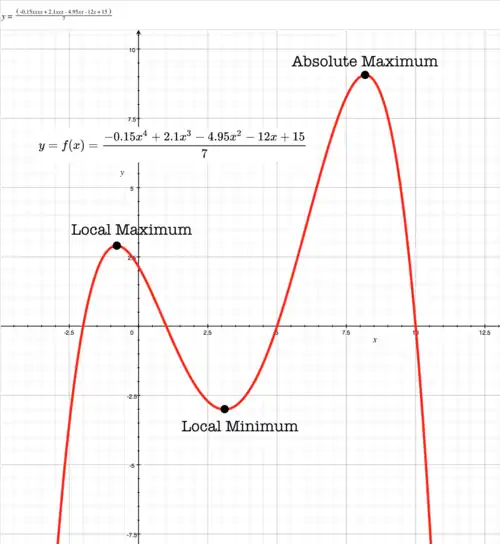
Maxima and minima
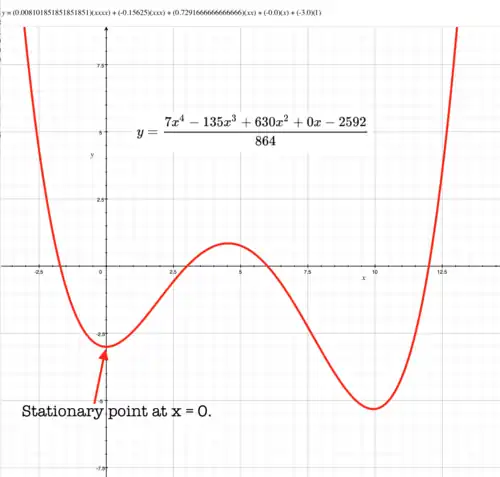
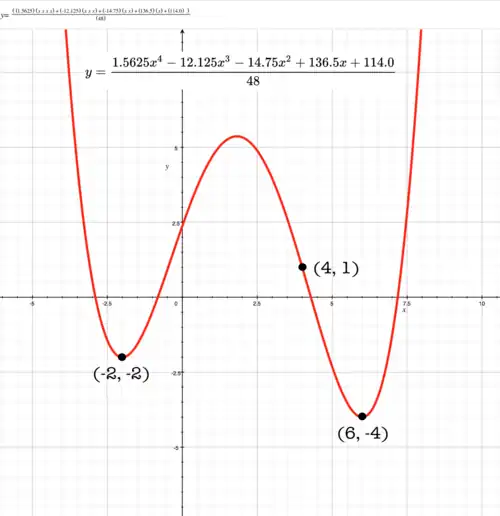
Quartic with 2 stationary points
|
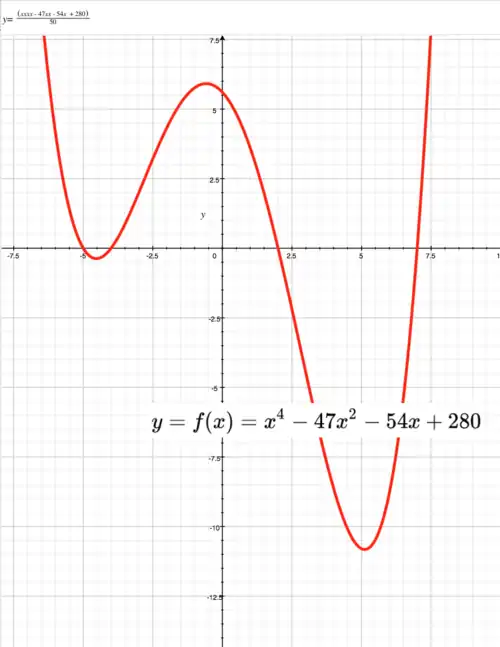
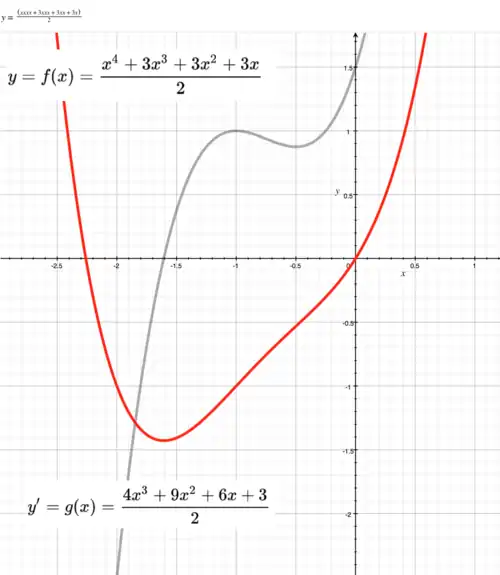
The simplest quartic function
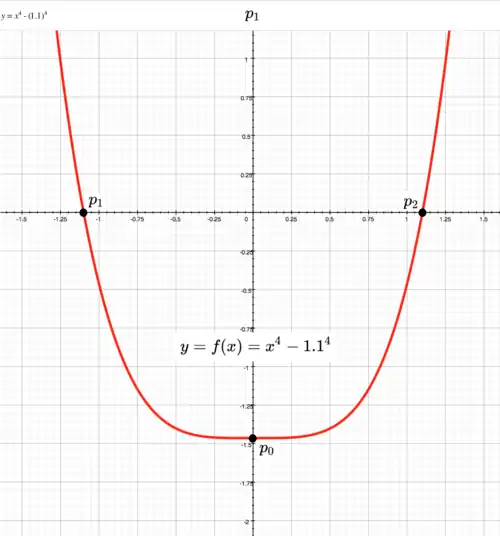 Graph of simplest quartic function.
Point is a root of Point is a root of Point is intercept of The simplest quartic function has coefficients Red line in diagram has equation: First derivative (not shown) of When There is a stationary point on when point Second derivative (not shown) of When There is a point of inflection on when For every non-zero value of is positive. To left and right of point is always concave up. Point is both local minimum and absolute minimum.
Solve:
This is equivalent to finding a root of function If you use Newton's method to find a root of this would be more efficient than solving |
Roots of equal absolute value
|
The standard quartic function: For in substitute Call this For in substitute Call this Combine and to eliminate and produce an equation in
If is a solution and function has 2 roots of form where
The method works with complex roots of equal absolute value:
|
Equal roots
|
Equal roots occur when the function and the slope of the function both equal zero.
where:
where:
where:
where:
where:
where:
From
+ 2048aaaaacddeeee - 768aaaaaddddeee - 1536aaaabcdddeee + 576aaaabdddddee
- 1024aaaacccddeee + 1536aaaaccddddee - 648aaaacdddddde + 81aaaadddddddd
+ 1152aaabbccddeee - 480aaabbcddddee + 18aaabbdddddde - 640aaabcccdddee
+ 384aaabccddddde - 54aaabcddddddd + 128aaacccccddee - 80aaaccccdddde
+ 12aaacccdddddd - 216aabbbbcddeee + 81aabbbbddddee + 144aabbbccdddee
- 86aabbbcddddde + 12aabbbddddddd - 32aabbccccddee + 20aabbcccdddde
- 3aabbccddddddwhich, by removing values (common to all values), may be reduced to: status = (
+ 2048aaaceeee - 768aaaddeee - 1536aabcdeee + 576aabdddee
- 1024aaccceee + 1536aaccddee - 648aacdddde + 81aadddddd
+ 1152abbcceee - 480abbcddee + 18abbdddde - 640abcccdee
+ 384abccddde - 54abcddddd + 128acccccee - 80accccdde
+ 12acccdddd - 216bbbbceee + 81bbbbddee + 144bbbccdee
- 86bbbcddde + 12bbbddddd - 32bbccccee + 20bbcccdde
- 3bbccdddd
)If there are at least 2 equal roots which may be calculated as shown below.
No equal roots
Exactly 2 equal roots
Exactly 3 equal roots
Four equal roots
Two pairs of equal roots
Summmary
Caution
|
Depressed quartic
|
A depressed quartic is any quartic function with any one or more of coefficients missing. Within this section a depressed quartic has coefficient missing. To produce the depressed quartic:
Let Substitute in expand and simplify:
where:
Be prepared for the possibility that any 1 or more of may be zero. Coefficient B missing
Coefficient C missing
Resolvent cubic
|
Solving quartic equation
This section presents 4 examples that show how to use the depressed quartic and the resolvent cubic to solve the quartic equation.
Four real roots
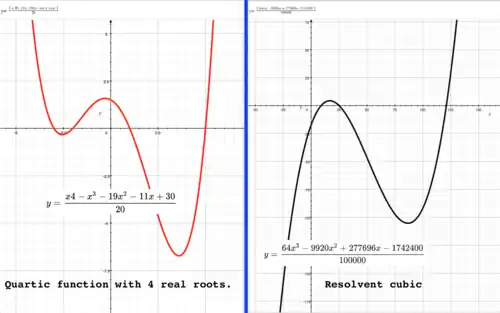 Graphs of quartic function with 4 real roots and associated resolvent cubic.
Resolvent cubic contains 3 real, positive roots. Calculate roots of: |
Calculate coefficients of depressed quartic:
a,b,c,d,e = 1,-1,-19,-11,30
A = 16*a*c - 6*b*b
B = 64*a*a*d - 32*a*b*c + 8*b*b*b
C = 256*a*a*a*e - 64*a*a*b*d + 16*a*b*b*c - 3*b*b*b*b
print (A,B,C)
-310 -1320 6669 |
Calculate coefficients of resolvent cubic:
P = 64
Q = 32*A
R = 4*A*A - 16*C
S = -B*B
print (P,Q,R,S)
64 -9920 277696 -1742400 |
Calculate roots of cubic function:
There are 3 real, positive roots:
Using 3 roots of calculate 4 roots of
# python code
for U in (9, 25, 121) :
print ('\nU =', U)
sqrtU = U ** 0.5
for u in (sqrtU, -sqrtU) :
V = -(A/2 + U) - B/(4*u)
v = V ** .5
for t in (u+v, u-v) :
x = (-b+t) / (4*a)
y = a*x**4 + b*x**3 + c*x**2 + d*x + e
print ('x:',x, '; y:',y)
U = 9
x: 5.0 ; y: 0.0
x: -3.0 ; y: 0.0
x: 1.0 ; y: 0.0
x: -2.0 ; y: 0.0
U = 25
x: 5.0 ; y: 0.0
x: -2.0 ; y: 0.0
x: 1.0 ; y: 0.0
x: -3.0 ; y: 0.0
U = 121
x: 5.0 ; y: 0.0
x: 1.0 ; y: 0.0
x: -2.0 ; y: 0.0
x: -3.0 ; y: 0.0Roots of are: |
All 3 values of produce the same results, but not in same sequence.
It is not necessary to calculate all 3 roots of resolvent cubic. Any one non-zero root is sufficient to do the job.
Two real and two complex roots
Example 1
 Graphs of quartic function with 2 real and 2 complex roots and associated resolvent cubic. Calculate roots of: |
|
Calculate coefficients of depressed quartic:
Calculate coefficients of resolvent cubic:
Calculate one real root of cubic function: is one real root. Choose Calculate roots of
|
Example 2
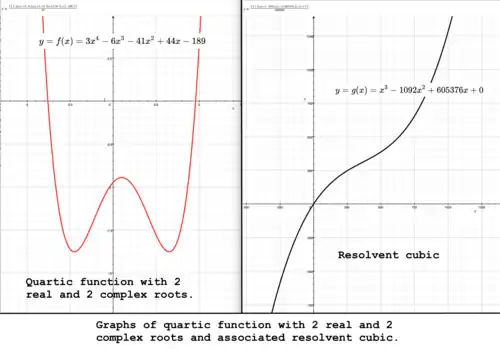
Coefficient of Calculate roots of: |
Calculate coefficients of depressed quartic:
a,b,c,d,e = 3, -6, -41, 44, -189
A = 16*a*c - 6*b*b
B = 64*a*a*d - 32*a*b*c + 8*b*b*b
C = 256*a*a*a*e - 64*a*a*b*d + 16*a*b*b*c - 3*b*b*b*b
print (A,B,C)
-2184, 0, -1229040Notice that coefficient |
Calculate coefficients of resolvent cubic:
P = 64
Q = 32*A
R = 4*A*A - 16*C
S = -B*B
print (P,Q,R,S)
1, -1092, 605376, 0Notice that coefficient |
Calculate roots of cubic function:
Roots are
Value cannot be used because it will cause error Divide by zero
at statement V = -(A/2 + U) - B/(4*u).
Calculate roots of
# python code
U = 546+554.3103823671355j
print ('\nU =',U)
sqrtU = U ** 0.5
for u in (sqrtU, -sqrtU) :
V = -(A/2 + U) - B/(4*u)
v = V ** 0.5
s1 = '\nu,v'
print (s1,eval(s1))
for t in (u+v, u-v) :
x = (-b+t)/(4*a)
# Check result. Expecting sum = 0.
sum = a*x**4 + b*x**3 + c*x**2 + d*x + e
print ('x =', x,'; sum =',sum)
U = (546+554.3103823671355j)
u,v ((25.729935131257832+10.771701901683684j), (25.729935131257832-10.771701901683684j))
x = (4.788322521876306 + 0j) ; sum = (1.9895196601282805e-13 + 0j)
x = (0.5 + 1.795283650280614j) ; sum = (5.684341886080802e-14 + 0j)
u,v ((-25.729935131257832-10.771701901683684j), (25.729935131257832-10.771701901683684j))
x = (0.5 - 1.795283650280614j) ; sum = (5.684341886080802e-14 + 0j)
x = (-3.7883225218763052 + 0j) ; sum = (1.7053025658242404e-13 + 0j)Values of are: |
Depressed quartic as quadratic
In this example coefficient of depressed quartic
Therefore, resolvent cubic can be ignored and depressed quartic processed as quadratic in
where
Solutions of this quadratic are:
T1,T2 = 2648.1182474349434, -464.11824743494344
t1 = T1 ** 0.5; t2 = ((-T2) ** 0.5) * 1j
for t in (t1,-t1,t2,-t2) :
x = (-b+t)/(4*a)
# Check result. Expecting sum = 0.
sum = a*x**4 + b*x**3 + c*x**2 + d*x + e
print ('x =', x,'; sum =',sum)
x = 4.788322521876305 ; sum = -1.7053025658242404e-13
x = -3.788322521876305 ; sum = -1.7053025658242404e-13
x = (0.5 + 1.7952836502806138j) ; sum = (-2.842170943040401e-14 + 0j)
x = (0.5 - 1.7952836502806138j) ; sum = (-2.842170943040401e-14 + 0j)or
x = 0.5 ± 4.288322521876305, 0.5 ± 1.7952836502806138jWith precision of 15, values of are same as those shown above.
When roots of quartic function are of form p ± q, p ± r,
coefficient of depressed function
Four complex roots
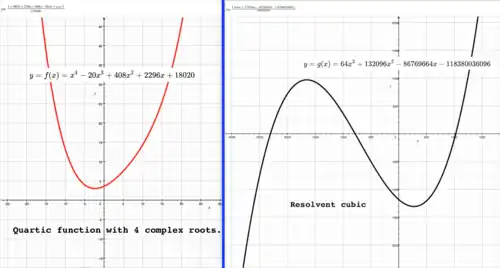 Graphs of quartic function with 4 complex roots and associated resolvent cubic. Calculate roots of: |
Calculate coefficients of depressed quartic:
4128 344064 9683200 |
Calculate coefficients of resolvent cubic:
64 132096 -86769664 -118380036096 |
Calculate one root of cubic function:
There are 3 real roots: Choose
Negative is chosen here to show that any 1 of the roots produces the correct result.
Calculate roots of
# python code
U = -784
u1 = 1j * (-U)**.5
for u in (u1, -u1) :
V = -(A/2 + U) - B/(4*u)
v = V**.5
for t in (u+v, u-v) :
x = (-b+t)/(4*a)
# Check result. Expecting sum = 0.
sum = a*x**4 + b*x**3 + c*x**2 + d*x + e
print ('x =', x,'; sum =',sum)
# python expresses complex numbers with 'j'.
x = (13+19j) ; sum = 0j
x = (-3-5j) ; sum = 0j
x = (13-19j) ; sum = 0j
x = (-3+5j) ; sum = 0j |
Quartic formula
The substitutions made above can be used to produce a formula for the solution of the quartic equation.
See main articles "The general case" or "General formula for roots."
|
Both links above point to formula for equation |
Given quartic equation: calculate the 4 values of
where:
|
Coefficients of depressed quartic:
|
|
Coefficients of resolvent cubic:
|
|
Coefficients of depressed cubic:
|
|
One root of resolvent cubic:
may be negative.
|
|
One root of quartic: may be positive or negative.
may be positive or negative.
|
Formula above produces one value of Python code below utilizes and to produce 4 values of and then, four values of
An example:
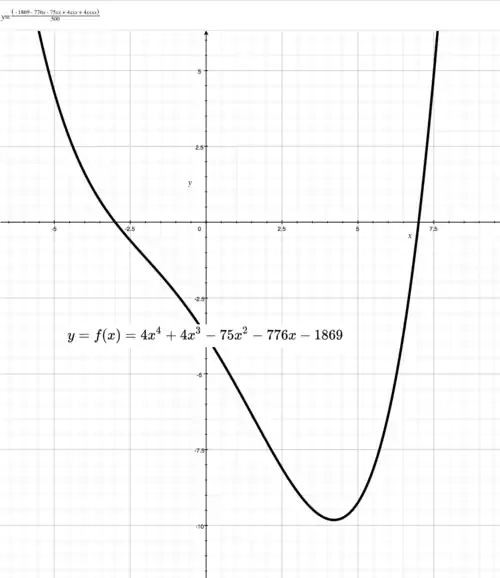 Graph of quartic function with 2 real roots. axis compressed for clarity. Calculate roots of # Python code.
a,b,c,d,e = 4, 4, -75, -776, -1869
values_of_t = [
t
# Coefficients of depressed quartic:
for A in (16*a*c - 6*b*b,)
for B in (64*a*a*d -32*a*b*c + 8*b*b*b,)
for C in (256*a*a*a*e - 64*a*a*b*d + 16*a*b*b*c - 3*b*b*b*b,)
# Coefficients of resolvent cubic:
for a1 in (64,)
for b1 in (32*A,)
for c1 in (4*A*A - 16*C,)
for d1 in (-B*B,)
for U in [
# The resolvent cubic:
(-b1+t1)/(3*a1)
# Coefficients of depressed resolvent cubic:
for A1 in (9*a1*c1 - 3*b1*b1,)
for B1 in (27*a1*a1*d1 - 9*a1*b1*c1 + 2*b1*b1*b1,)
# One root of resolvent cubic:
for C1 in (-A1/3,)
for Δ in (B1*B1 - 4*C1*C1*C1,)
for δ in (Δ**0.5,)
for W in ((-B1 + δ)/2,)
for w in (W**(1/3),)
for t1 in (w + C1/w,) # See note below.
]
# Prepare to calculate 4 values of t.
for u1 in (U**.5,)
for v1 in ( -(A/2 + U) ,)
# Calculate 4 values of t.
for u in (u1, -u1,)
for V in ( v1 - B/(4*u),)
for v in (V**.5,)
for t in (u+v, u-v)
]
print ('values_of_t =', values_of_t)
# Python code.
# Calculate 4 separate roots.
values_of_x = [
(-b + t)/(4*a)
for t in values_of_t
]
print ('values_of_x =', values_of_x)
values_of_x = [7, -3, (-2.5 + 4j), (-2.5 - 4j)]
In python the imaginary part of a complex number is shown with instead of If contains 4 equal roots and If contains 3 or more equal roots, statement Before using this formula, check for equal roots as in "Exactly 3 equal roots" above.
|
In practice
|
The following Python code implements the quartic formula. However, under statement
Examples
|
Two Conic Sections
Examples of conic sections include: ellipse, circle, parabola and hyperbola.
This section presents examples of two conic sections, circle and ellipse, and how to calculate the coordinates of the point/s of intersection, if any, of the two sections.
Let one section with name have equation
Let other section with name have equation
Because there can be as many as 4 points of intersection, a special "resolvent" quartic function is used to calculate the coordinates of the point/s of intersection.
Coefficients of associated "resolvent" quartic are calculated as follows:
# python code
def intersection_of_2_conic_sections (abcdef, ABCDEF) :
'''
A_,B_,C_,D_,E_ = intersection_of_2_conic_sections (abcdef, ABCDEF)
where A_,B_,C_,D_,E_ are coefficients of associated resolvent quartic function:
y = f(x) = A_*x**4 + B_*x**3 + C_*x**2 + D_*x + E_
'''
A,B,C,D,E,F = ABCDEF
a,b,c,d,e,f = abcdef
G = ((-1)*(B)*(a) + (1)*(A)*(b))
H = ((-1)*(B)*(d) + (1)*(D)*(b))
I = ((-1)*(B)*(f) + (1)*(F)*(b))
J = ((-1)*(C)*(a) + (1)*(A)*(c))
K = ((-1)*(C)*(d) + (-1)*(E)*(a) + (1)*(A)*(e) + (1)*(D)*(c))
L = ((-1)*(C)*(f) + (-1)*(E)*(d) + (1)*(D)*(e) + (1)*(F)*(c))
M = ((-1)*(E)*(f) + (1)*(F)*(e))
g = ((-1)*(C)*(b) + (1)*(B)*(c))
h = ((-1)*(E)*(b) + (1)*(B)*(e))
i = ((-1)*(A)*(b) + (1)*(B)*(a))
j = ((-1)*(D)*(b) + (1)*(B)*(d))
k = ((-1)*(F)*(b) + (1)*(B)*(f))
A_ = ((-1)*(J)*(g) + (1)*(G)*(i))
B_ = ((-1)*(J)*(h) + (-1)*(K)*(g) + (1)*(G)*(j) + (1)*(H)*(i))
C_ = ((-1)*(K)*(h) + (-1)*(L)*(g) + (1)*(G)*(k) + (1)*(H)*(j) + (1)*(I)*(i))
D_ = ((-1)*(L)*(h) + (-1)*(M)*(g) + (1)*(H)*(k) + (1)*(I)*(j))
E_ = ((-1)*(M)*(h) + (1)*(I)*(k))
str1 = 'y = ({})x^4 + ({})x^3 + ({})x^2 + ({})x + ({}) '.format(A_,B_,C_,D_,E_)
print (str1)
return A_,B_,C_,D_,E_
With no common point
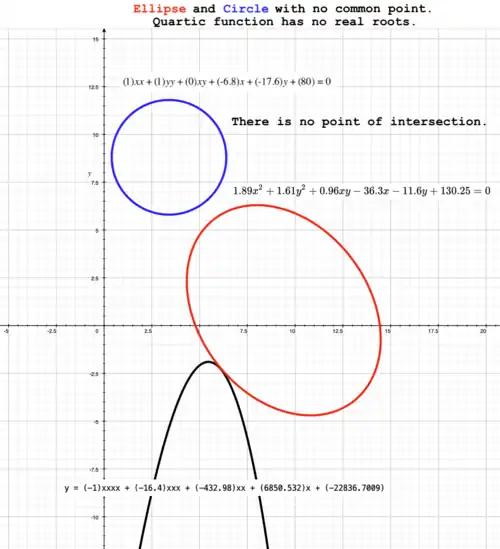 Two conic sections with no common point.
Resolvent quartic function (black curve) has no real roots. axis of quartic function is compressed to illustrate shape of curve. Let ellipse (red curve) have equation: Let circle (blue curve) have equation: Then, resolvent quartic function (black curve) has equation:
has no real roots. Therefore, there is no point of intersection. |
With one common point
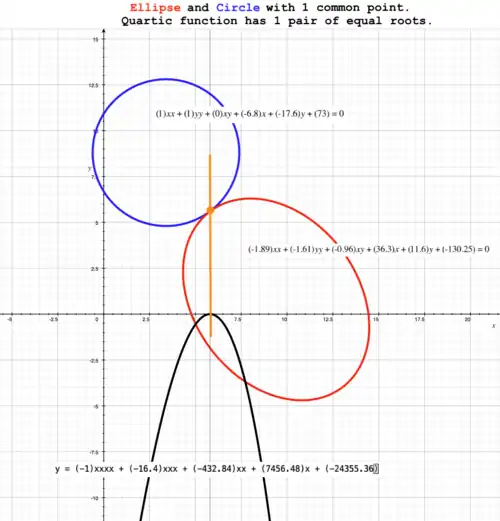 Two conic sections with one common point.
Resolvent quartic function (black curve) has two equal, real roots. axis of quartic function is compressed to illustrate shape of curve. Let ellipse (red curve) have equation: Let circle (blue curve) have equation: Then, resolvent quartic function (black curve) has equation:
Roots of are: has 2 equal, real roots at effectively 1 real root where Therefore, there is one point of intersection where |
With two common points
Example 1
 Two conic sections with two common points.
Resolvent quartic function (black curve) has two unique, real roots. axis of quartic function is compressed to illustrate shape of curve. Let ellipse (red curve) have equation: Let circle (blue curve) have equation: Then, resolvent quartic function (black curve) has equation:
Roots of are: has 2 unique, real roots at Therefore, there are two points of intersections where |
Example 2
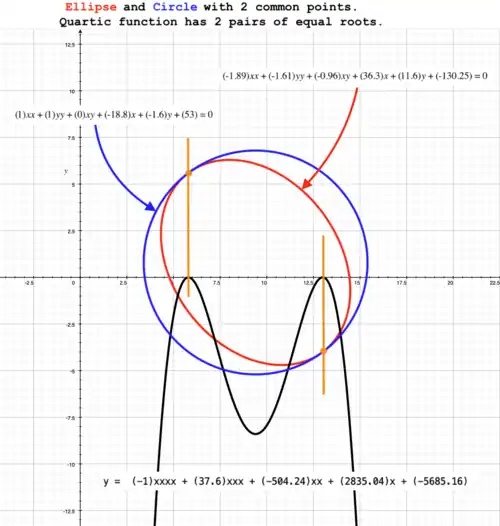 Two conic sections with two common points.
Resolvent quartic function (black curve) has two pairs of equal roots. axis of quartic function is compressed to illustrate shape of curve. Let ellipse (red curve) have equation: Let circle (blue curve) have equation: Then, resolvent quartic function (black curve) has equation:
Roots of are: has 2 pairs of equal roots at effectively 2 real roots. Therefore, there are two points of intersection where |
With 3 common points
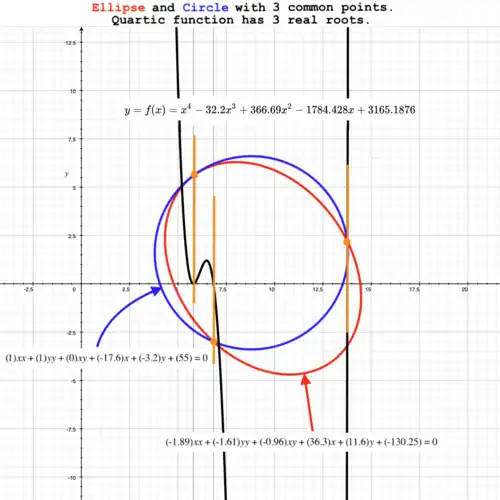 Two conic sections with three common points.
Resolvent quartic function (black curve) has one pair of equal roots and 2 unique, real roots. Let ellipse (red curve) have equation: Let circle (blue curve) have equation: Then, resolvent quartic function (black curve) has equation:
Roots of are: has 1 pair of equal roots at and 2 unique, real roots at effectively 3 real roots. Therefore, there are three points of intersection where |
With 4 common points
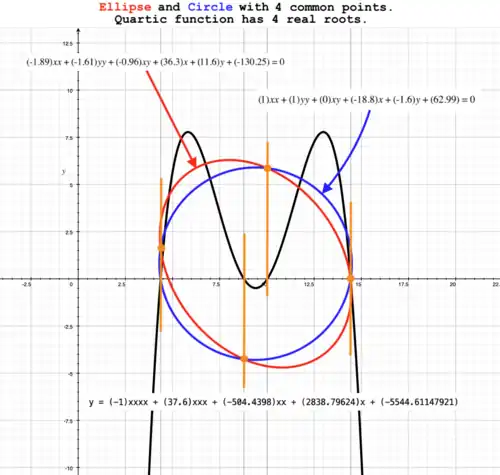 Two conic sections with four common points.
Resolvent quartic function (black curve) has 4 unique, real roots. axis of quartic function is compressed to illustrate shape of curve. Let ellipse (red curve) have equation: Let circle (blue curve) have equation: Then, resolvent quartic function (black curve) has equation:
Roots of are: has 4 real roots as shown above. Therefore, there are four points of intersection where |