Line integral

Introduction

The Curve, Line, Path or Contour integral expands the standard integral term for the Integration in the complex plane (Complex Analysis) or in the multidimensional space $\mathbb {R} ^{n}$ or $\mathbb {C} ^{n}$ . The path, the line or the curve, via which is integrated, is called the integration path^[1]. The line integral over a closed path are written with the symbol ${\textstyle \textstyle \oint }$ .

Real-valued Line Integrale

A path ${\textstyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$ is given which is imaged from an interval (e.g. interpreted as a time interval) into the vector space ${\textstyle \mathbb {R} ^{n}}$ . ${\textstyle \gamma (t)\in \mathbb {R} ^{n}}$ indicates the place where the value is ${\textstyle t\in [a,b]}$ . The difference is

Line integral first type and
Line integral second type.

Pathintegral first type

Animation for a line integral of first type over a scalar field

The path integral of a continuous Function

{\textstyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }

along a continuously differentiable piece path ${\textstyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$ is defined as

\int \limits _{\gamma }\!f\,\mathrm {d} s:=\int \limits _{a}^{b}\!f(\gamma (t))\,\|{\gamma \,}'(t)\|_{2}\,\mathrm {d} t.

Deduction of the path

${\textstyle {\gamma \,}'}$ refers to the derivation from ${\textstyle \gamma }$ to ${\textstyle t}$ . ${\textstyle \gamma (t)\in \mathbb {R} ^{n}}$ and ${\textstyle {\gamma \,}'(t)\in \mathbb {R} ^{n}}$ are a vectors. The derivation vector ${\textstyle {\gamma \,}'(t)\in \mathbb {R} ^{n}}$ indicates the change behavior in each component function of ${\textstyle \gamma =(\gamma _{1},\dots ,\gamma _{n})}$ .

Remark - Component functions

The component functions ${\textstyle \gamma _{i}:[a,b]\to \mathbb {R} }$ are illustrations for which the derivation with the knowledge from the real analysis can be calculated.

Example of a path and its derivation

A differentiable path is defined first ${\textstyle \gamma }$ with

{\displaystyle {\begin{array}{rrcl}\gamma

The track of the path forms an ellipse with the half axes 5 and 3.

Derivation of the path in the two-dimensional space

The derivation ${\textstyle {\gamma }'}$ of the path ${\textstyle \gamma }$ results directly from the derivation of the component functions

{\begin{array}{rrcl}{\gamma }':&[0,2\pi ]&\rightarrow &\mathbb {R} ^{2}\\&t&\mapsto &{\gamma }'\left(t\right)={\begin{pmatrix}-5\cdot \sin(t)\\3\cdot \cos(t)\end{pmatrix}}\end{array}}

Example - Deduction of the Way in the Three-dimensional Space

Now a vector is ${\textstyle \gamma (t)=(\cos(t),\sin(t),t)\in \mathbb {R} ^{3}}$ and ${\textstyle {\gamma \,}'(t)=(-\sin(t),\cos(t),1)\in \mathbb {R} ^{3}}$ . The derivation vector ${\textstyle {\gamma \,}'(t)\in \mathbb {R} ^{3}}$ indicates the change behavior in each component function of ${\textstyle \gamma =(\gamma _{1},\gamma _{2},\gamma _{3})}$ .

Task

Draw the trail of the path in ${\textstyle \mathbb {R} ^{2}}$ (Ellipse) and plotted the trail of the path in ${\textstyle \mathbb {R} ^{3}}$ with CAS4Wiki plots.

Vector length of the derivation vector of the path

${\textstyle \|{\gamma \,}'(t)\|_{2}}$ indicates the Euclidian norm of the vector ${\textstyle {\gamma \,}'(t)\in \mathbb {R} ^{n}}$ .

Picture of the path - track

The image set ${\textstyle {\mbox{trace}}(\gamma ):={\mathcal {C}}:=\gamma ([a,b])}$ of one piece differentiable curve in ${\textstyle \mathbb {R} ^{n}}$ should not be confused with the graph of a curve which is a part of the ${\textstyle [a,b]\times \mathbb {R} ^{n}}$ .

Notes

An example of such a function ${\textstyle f}$ is a scalar field with cartesischen coordinaten.
A path ${\textstyle \gamma }$ can pass through a curve ${\textstyle {\mathcal {C}}}$ either as a whole or only in sections several times.
For ${\textstyle f\equiv 1}$ , the path integral of the first type gives the length of the path ${\textstyle \gamma }$ .
The path ${\textstyle \gamma }$ forms, inter alia ${\textstyle a\in \mathbb {R} }$ on the starting point of the curve and ${\textstyle b\in \mathbb {R} }$ on its end point.
${\textstyle t\in [a,b]}$ is an element of the definition set of ${\textstyle \gamma }$ and is generally not' for time. ${\textstyle \mathrm {d} t}$ is the corresponding Differential.

Pathintegral second type

Visualization of a line integral of second type over Gradient vector field

The line integral over a continuous gradient vector field

{\textstyle \mathbf {f} \colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}}

with a curve also parameterized in this way is defined as the integral over the scalar product of ${\textstyle \mathbf {f} \circ \gamma }$ and ${\textstyle \gamma \,'}$ :

{\textstyle \int \limits _{\gamma }\!\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x}

Influence of parameterization

If ${\textstyle \gamma \colon [a,b]\to \mathbb {R} ^{n}}$ and ${\textstyle \eta \colon [c,d]\to \mathbb {R} ^{n}}$ 'simplified' (d. h, ${\textstyle \gamma _{|(a,b)}}$ and ${\textstyle \eta _{|(c,d)}}$ are identical This justifies the name curve integral; if the direction of integration is visible or irrelevant, the path in the notation can be suppressed.

Curve integrals

Since a curve ${\textstyle {\mathcal {C}}}$ is the image of a path ${\textstyle \gamma }$ , the definitions of the curve integrals essentially correspond to the path integrals.

Curve integral 1. type

{\textstyle \int \limits _{\mathcal {C}}\!f\,\mathrm {d} s:=\int \limits _{a}^{b}\!f(\gamma (t))\cdot \|{{\gamma }\,}'(t)\|_{2}\,\mathrm {d} t}

Curve integral 2. type

{\textstyle \int \limits _{\mathcal {C}}\mathbf {f} (\mathbf {x} )\cdot \mathrm {d} \mathbf {x}

Length of curve

A special case is again the length of the curve ${\textstyle {\mathcal {C}}}$ parameterized by ${\textstyle \gamma }$ :

{\textstyle {\mathcal {L}}({\mathcal {C}})=\int \limits _{\mathcal {C}}1\,\mathrm {d} s=\int \limits _{a}^{b}\|{\gamma \,}'(t)\|_{2}\,\mathrm {d} t}

Displacement element and length element

The expression occurring in the first type of curves

{\textstyle \mathrm {d} s=\|{\gamma \,}'(t)\|_{2}\,\mathrm {d} t}

is called scalar path element' or 'length element.The expression occurring in the second type of curve integrals

\mathrm {d} \mathbf {x} ={\gamma \,}'(t)\,\mathrm {d} t

is called 'vectorial path element'.

Rules of Procedure

Be ${\textstyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )}$ , ${\textstyle \int \limits _{\gamma }\mathbf {g} (\mathbf {x} )}$ Curve integrals of the same type (i.e. either both first or second type), be the original image of the two functions ${\textstyle \mathbf {f} }$ and ${\textstyle \mathbf {g} }$ of the same dimension and be (698104789). The following rules apply to ${\textstyle \alpha }$ , ${\textstyle \beta \in \mathbb {R} }$ and ${\textstyle c\in \mathbb {[} a,b]}$ :

${\textstyle \alpha \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )+\beta \int \limits _{\gamma }\mathbf {g} (\mathbf {x} )=\int \limits _{\gamma }(\alpha \mathbf {f} (\mathbf {x} )+\beta \mathbf {g} (\mathbf {x} ))}$
${\textstyle \int \limits _{\gamma }\mathbf {f} (\mathbf {x} )=\int \limits _{\gamma |_{[a,c]}}\mathbf {f} (\mathbf {x} )+\int \limits _{\gamma |_{[c,b]}}\mathbf {f} (\mathbf {x} )}$

Notation for curve integrals of closed curves

If ${\textstyle \gamma }$ is a closed way, you write

instead of

{\textstyle \displaystyle \int \limits _{\gamma }}

also

{\textstyle \displaystyle \oint \limits _{\gamma }}

and similar for closed curves ${\textstyle {\mathcal {C}}}$

instead of

{\textstyle \displaystyle \int \limits _{\mathcal {C}}}

also

{\textstyle \displaystyle \oint \limits _{\mathcal {C}}}

.

With the circle in the Integral one would like to make clear that ${\textstyle \gamma }$ is closed. The only difference is in the notation.

Examples

If ${\textstyle {\mathcal {C}}}$ is the graph of a function ${\textstyle f\colon [a,b]\to \mathbb {R} }$ , this curve will be passed through the path

{\textstyle \gamma \colon [a,b]\to \mathbb {R} ^{2},\quad t\mapsto (t,f(t))}

parametrized with

(t,f(t))\in \mathbb {R} ^{3}

. About

{\textstyle \|\gamma {\,}'(t)\|_{2}={\sqrt {1+f'(t)^{2}}}}

the length of the curve is equal

{\textstyle \int \limits _{\mathcal {C}}\mathrm {d} s=\int \limits _{a}^{b}{\sqrt {1+f'(t)^{2}}}\,\mathrm {d} t.}

A ellipse with large half-axis ${\textstyle a}$ and small half-axis ${\textstyle b}$ is parameterized by ${\textstyle (a\cos t,\,b\sin t)}$ for ${\textstyle t\in [0,2\pi ]}$ . Your scope is therefore

{\textstyle \int \limits _{0}^{2\pi }{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,\mathrm {d} t=4a\int \limits _{0}^{\frac {\pi }{2}}{\sqrt {1-\varepsilon ^{2}\cos ^{2}t}}\;\mathrm {d} t}

.

In this case

{\textstyle \varepsilon }

refers to the numerical eccenttricity

{\textstyle {\sqrt {1-b^{2}/a^{2}}}}

of the ellipse. The integral on the right is referred to as elliptic tntegral due to this connection.

Path Independency on Integral

If a vector field ${\textstyle \mathbf {F} }$ is a Gradient field, i.e.

{\textstyle \mathbf {\nabla } V=\mathbf {F} }

,

This applies to derivation of function composition of ${\textstyle V}$ and ${\textstyle \mathbf {r} (t)}$

{\textstyle {\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {r} (t))=\mathbf {\nabla } V(\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)=\mathbf {F} (\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)}

,

which exactly corresponds to the integral of the path integral over ${\textstyle \mathbf {F} }$ to ${\textstyle \mathbf {r} (t)}$ .

Dependence of integral boundaries 1

This follows for a given curve ${\textstyle {\mathcal {S}}}$

{\textstyle \int \limits _{\mathcal {S}}\mathbf {F} (\mathbf {x} )\cdot \,\mathrm {d} \mathbf {x} =\int \limits _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot {\dot {\mathbf {r} }}(t)\,\mathrm {d} t=\int \limits _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} t}}V(\mathbf {r} (t))\,\mathrm {d} t=V(\mathbf {r} (b))-V(\mathbf {r} (a)).}

Visualization

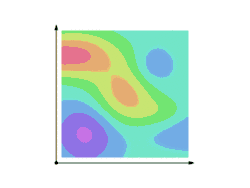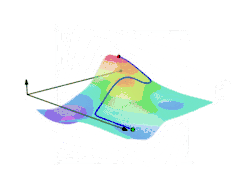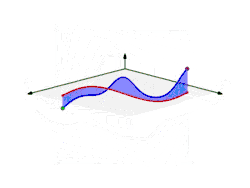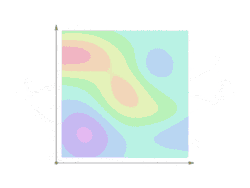
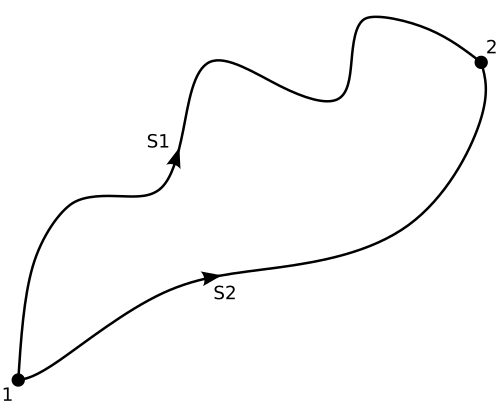
The following image show two arbitrary curves $S1$ and $S2$ in a Gradient vector field connecting point $1$ with point $2$ .

two arbitrary curves 'S1' and 'S2' in a Gradient vector field connecting point 1 with point 2.

Dependence of integral boundaries 2

This means that the integral of ${\textstyle \mathbf {F} }$ over ${\textstyle {\mathcal {S}}}$ depends solely on points ${\textstyle \mathbf {r} (b)}$ and ${\textstyle \mathbf {r} (a)}$ and the path between them is irrelevant to the result. For this reason, the integral of a gradient field is referred to as “displaced”.

Remark - closed paths - Ringintegral

In particular, the ring integral applies to the closed curve ${\textstyle {\mathcal {S}}}$ with two arbitrary paths ${\textstyle {\mathcal {S}}_{1}}$ and ${\textstyle {\mathcal {S}}_{2}}$ :

{\textstyle \oint \limits _{\mathcal {S}}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} =\int \limits _{1,{\mathcal {S}}_{1}}^{2}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} +\int \limits _{2,{\mathcal {S}}_{2}}^{1}\mathbf {F} (\mathbf {x} )\,\mathrm {d} \mathbf {x} =0}

Application in Physics

This is particularly important in Physics, since, for example, the Gravitation has these properties. Since the energy in these force fields is always a conservation variable, they are referred to in physics as conservative force.

Scaler fields - Potential energy

The scalar field ${\textstyle V}$ is the Potential or the potential Energy. Conservative force fields receive the mechanical energy, i.e. the sum of kinetic Energy and potential energy. According to the above integral, a work of 0 J is applied on a closed curve overall.

Number of revolutions

Path independence can also be shown with the application of the Integrability condition.

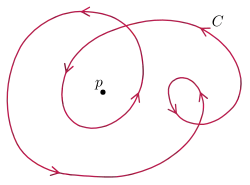
This curve has winding number two around the point p.

if the vector field is not possible as a gradient field only in a (small) environment ${\textstyle U}$ of a point, the closed path integral of curves outside ${\textstyle U}$ is proportional to the number of turns around this point and otherwise independent of the exact curve (see Algebraic Topology: Methodology).

Remark - Complex pathintegrale

If ${\textstyle \mathbb {R} ^{n}}$ is replaced by ${\textstyle \mathbb {C} }$ , complex path integrals are treated which are treated in the Complex Analysis.

Literature

Harro Heuser: Lehrbuch der Analysis – Teil 2. 1981, 5. Auflage, Teubner 1990, ISBN 3-519-42222-0. p. 369, Theorem 180.1; p. 391, Theorem 184.1; p. 393, Theorem 185.1.

References

↑ Klaus Knothe, Heribert Wessels: Finite Elemente. Eine Einführung für Ingenieure. 3. Auflage. 1999, ISBN 3-540-64491-1, S. 524.

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Calculus' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Line%20integral
see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

Source: Wegintegral - URL: https://en.wikiversity.org/wiki/Wegintegral
Date: 11/20/2024

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[cite2-1] Klaus Knothe, Heribert Wessels: Finite Elemente. Eine Einführung für Ingenieure. 3. Auflage. 1999, ISBN 3-540-64491-1, S. 524.

[1]