OpenStax University Physics/V1/Formulas

Introduction: 

1. Units_and_Measurement:  The base SI units are mass: kg (kilogram); length: m (meter); time: s (second). ^[1]

Percent error is ${\displaystyle (\delta A/A)\times 100\%}$

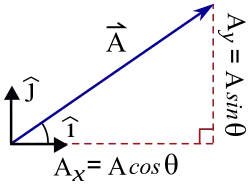
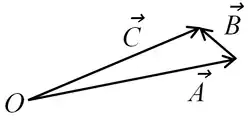
2. Vectors: Vector ${\displaystyle {\vec {A}}=A_{x}\,{\hat {i}}+A_{y}\,{\hat {j}}+A_{z}\,{\hat {k}}}$ involves components (A_x,A_y,A_z) and ^[2] unit vectors.^[3] ▭ If ${\displaystyle {\vec {A}}+{\vec {B}}={\vec {C}}}$, then A_x+B_x=C_x, etc, and vector subtraction is defined by ${\displaystyle {\vec {B}}={\vec {C}}-{\vec {A}}}$.

▭ The two-dimensional displacement from the origin is ${\displaystyle {\vec {r}}=x{\hat {i}}+y{\hat {j}}}$. The magnitude is ${\displaystyle A\equiv |{\vec {A}}|={\sqrt {A_{x}^{2}+A_{y}^{2}}}}$. The angle (phase) is ${\displaystyle \theta =\tan ^{-1}{(y/x)}}$. ▭ Scalar multiplication ${\displaystyle \alpha {\vec {A}}=\alpha A_{x}{\hat {i}}+\alpha A_{y}{\hat {j}}+...\quad }$ ▭ Any vector divided by its magnitude is a unit vector and has unit magnitude: ${\displaystyle |{\hat {V}}|=1}$ where ${\displaystyle {\hat {V}}\equiv {\vec {V}}/V}$ ▭ Dot product ${\displaystyle {\vec {A}}\cdot {\vec {B}}=AB\cos \theta =A_{x}B_{x}+A_{y}B_{y}+...\quad }$ and ${\displaystyle {\vec {A}}\cdot {\vec {A}}=A^{2}}$ ▭ Cross product ${\displaystyle {\vec {A}}={\vec {B}}\times {\vec {C}}\Rightarrow }$ ${\displaystyle A_{\alpha }=B_{\beta }C_{\gamma }-C_{\gamma }A_{\beta }}$ where ${\displaystyle (\alpha ,\beta ,\gamma )}$ is any cyclic permutation of ${\displaystyle (x,y,z)}$, i.e., (α,β,γ) represents either (x,y,z) or (y,z,x) or (z,x,y). ▭ Cross-product magnitudes obey ${\displaystyle A=BC\sin \theta }$ where ${\displaystyle \theta }$ is the angle between ${\displaystyle {\vec {B}}}$ and ${\displaystyle {\vec {C}}}$, and ${\displaystyle {\vec {A}}\perp \{{\vec {B}},{\vec {C}}\}}$ by the right hand rule. ▭ Vector identities ${\displaystyle \;c(\mathbf {A} +\mathbf {B} )=c\mathbf {A} +c\mathbf {B} \quad }$ ▭ ${\displaystyle \mathbf {A} +\mathbf {B} =\mathbf {B} +\mathbf {A} \quad }$ ▭ ${\displaystyle \mathbf {A} +(\mathbf {B} +\mathbf {C} )=(\mathbf {A} +\mathbf {B} )+\mathbf {C} \quad }$ ▭ ${\displaystyle \mathbf {A} \cdot \mathbf {B} =\mathbf {B} \cdot \mathbf {A} \quad }$ ▭ ${\displaystyle \mathbf {A} \times \mathbf {B} =\mathbf {-B} \times \mathbf {A} \quad }$ ▭ ${\displaystyle \left(\mathbf {A} +\mathbf {B} \right)\cdot \mathbf {C} =\mathbf {A} \cdot \mathbf {C} +\mathbf {B} \cdot \mathbf {C} \quad }$ ^[4] 3. Motion_Along_a_Straight_Line:  ^[5] ▭ Average velocity ${\displaystyle {\bar {v}}=\Delta x/\Delta t\rightarrow v=dx/dt}$ (instantaneous velocity) ▭ Acceleration ${\displaystyle {\bar {a}}=\Delta v/\Delta t\rightarrow a=dv/dt}$. ▭ WLOG set ${\displaystyle \Delta t=t\;}$ and ${\displaystyle \Delta x=x-x_{0}\;}$ if ${\displaystyle t_{i}=0}$. Then ${\displaystyle \Delta v=v-v_{0}}$, and ${\displaystyle \;v(t)=\int _{0}^{t}a(t')dt'+v_{0}}$, ${\displaystyle \;x(t)=\int _{0}^{t}v(t')dt'+x_{0}=x_{0}+{\bar {v}}t}$^[6] ▭ At constant acceleration: ${\displaystyle {\bar {v}}={\tfrac {v_{0}+v}{2}},\quad v=v_{0}+at,\quad x=x_{0}+v_{0}t+{\tfrac {1}{2}}at^{2},\,}$ ${\displaystyle v^{2}=v_{0}^{2}+2a\Delta x}$. ▭ For free fall, replace ${\displaystyle x\rightarrow y}$ (positive up) and ${\displaystyle a\rightarrow -g}$, where ${\displaystyle g}$ = 9.81 m/s² at Earth's surface). 4. Motion_in_Two_and_Three_Dimensions:  Instantaneous velocity: ${\displaystyle {\vec {v}}(t)=v_{x}(t){\hat {i}}+v_{y}(t){\hat {j}}+v_{z}(t){\hat {k}}={\frac {dx}{dt}}{\hat {i}}+{\frac {dy}{dt}}{\hat {j}}+{\frac {dz}{dt}}{\hat {k}}}$ ▭ ${\displaystyle {\vec {v}}(t)=\lim _{\Delta t\rightarrow 0}{\tfrac {\Delta {\vec {r}}}{\Delta t}}=\lim _{\Delta t\rightarrow 0}{\tfrac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}}$, where ${\displaystyle {\vec {r}}(t)=x(t){\hat {i}}+y(t){\hat {j}}+z(t){\hat {k}}}$ ▭ Acceleration ${\displaystyle {\vec {a}}=a_{x}{\hat {i}}+a_{y}{\hat {j}}+a_{z}{\hat {k}}}$, where ${\displaystyle a_{x}(t)=dv_{x}/dt=d^{2}x/dt^{2}}$. ^[7] ▭ Uniform circular motion: position ${\displaystyle \,{\vec {r}}(t)}$, velocity ${\displaystyle \,{\vec {v}}(t)=d{\vec {r}}(t)/dt}$, and acceleration ${\displaystyle \,{\vec {a}}(t)=d{\vec {v}}(t)/dt}$: ${\displaystyle {\vec {r}}=A\cos \omega t{\hat {i}}+A\sin \omega t{\hat {j}}\,,\,}$ ${\displaystyle {\vec {v}}=-A\omega \sin \omega t{\hat {i}}+A\omega \cos \omega t{\hat {j}}\,,\,}$ ${\displaystyle {\vec {a}}=-A\omega ^{2}\cos \omega t{\hat {i}}-A\omega ^{2}\sin \omega t{\hat {j}}\,.}$ Note that if ${\displaystyle A=r}$ then ${\displaystyle |{\vec {a}}|=a_{C}=\omega ^{2}r=v^{2}/r}$ where ${\displaystyle v\equiv |{\vec {v}}|=\omega r}$. ^[8] ▭ Relative motion: ^[9] ${\displaystyle \,{\vec {v}}_{PS}={\vec {v}}_{PS'}+{\vec {v}}_{S'S}}$, ^[10] 5. Newton's_Laws_of_Motion:  ^[11]${\displaystyle \;m{\vec {a}}=d{\vec {p}}/dt=\sum {\vec {F}}_{j}}$, where ${\displaystyle {\vec {p}}=m{\vec {v}}}$ is momentum, ^[12] ${\displaystyle \sum {\vec {F}}_{j}}$ is the sum of all forces This sum needs only include external forces ^[13]${\displaystyle {\vec {F}}_{AB}=-{\vec {F}}_{BA}}$.^[14]

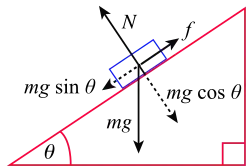
▭ Weight${\displaystyle ={\vec {w}}=m{\vec {g}}}$. ▭ normal force^[15] ${\displaystyle |{\vec {N}}|=N=mg\cos \theta }$^[16] ▭ ^[17]${\displaystyle F=-kx}$ where ${\displaystyle k}$ is the spring constant. 6. Applications_of_Newton's_Laws:  ${\displaystyle f_{s}\leq \mu _{s}N{\text{ and }}f_{k}=\mu _{k}N}$: ${\displaystyle \,f=}$ friction, ${\displaystyle \mu _{s,k}=}$ coefficient of (static,kinetic) friction, ${\displaystyle N=}$ normal force. ▭ Centripetal force${\displaystyle F_{c}=mv^{2}/r=mr\omega ^{2}}$ for uniform circular motion. Angular velocity ${\displaystyle \omega }$ is measured in radians per second. ^[18]▭ Drag equation ${\displaystyle F_{D}={\tfrac {1}{2}}C\rho Av^{2}}$ where ${\displaystyle C=}$ Drag coefficient, ${\displaystyle \rho =}$ mass density, ${\displaystyle A=}$ area, ${\displaystyle v=}$ speed. Holds approximately for large Reynold's number^[19] 7. Work_and_Kinetic_Energy:  Infinitesimal work^[20] ${\displaystyle dW={\vec {F}}\cdot d{\vec {r}}=|{\vec {F}}|\,|d{\vec {r}}|\cos \theta }$ leads to the path integral ${\displaystyle W_{AB}=\int _{A}^{B}{\vec {F}}\cdot d{\vec {r}}}$ ▭ Work done from A→B by friction ${\displaystyle -f_{k}|\ell _{AB}|,\;}$gravity ${\displaystyle -mg(y_{B}-y_{A}),\;}$ and spring ${\displaystyle -{\tfrac {1}{2}}k\left(x_{B}^{2}-x_{A}^{2}\right)}$ ▭ Work-energy theorem: ^[21] ${\displaystyle W_{net}=K_{B}-K_{A}}$ where kinetic energy ${\displaystyle =K={\tfrac {1}{2}}mv^{2}={\frac {p^{2}}{2m}}}$. ▭ Power${\displaystyle =P=dW/dt={\vec {F}}\cdot {\vec {v}}}$. 8. Potential_Energy_and_Conservation_of_Energy:  Potential Energy: ${\displaystyle \Delta U_{AB}=U_{B}-U_{A}=-W_{AB}}$; PE at ${\displaystyle {\vec {r}}}$ WRT ${\displaystyle {\vec {r}}_{0}}$ is ${\displaystyle \Delta U=U({\vec {r}})-U({\vec {r}}_{0})}$ ${\displaystyle U=mgy+{\mathcal {C}}}$ (gravitational PE Earth's surface. ${\displaystyle U={\tfrac {1}{2}}kx^{2}+{\mathcal {C}}}$ (ideal spring) ▭ Conservative force: ${\displaystyle \oint {\vec {F}}_{\text{cons}}\cdot d{\vec {r}}=0}$. In 2D, ${\displaystyle {\vec {F}}(x,y)}$ is conservative if and only if ${\displaystyle {\vec {F}}=-(\partial U/\partial x)\,{\hat {i}}-(\partial U/\partial y)\,{\hat {j}}\iff \partial F_{x}/\partial y=\partial F_{y}/\partial x}$ ▭ Mechanical energy is conserved if no non-conservative forces are present: ${\displaystyle 0=W_{nc,AB}=\Delta (K+U)_{AB}=\Delta E_{AB}}$ 9. Linear_Momentum_and_Collisions:  ${\displaystyle {\vec {F}}(t)=d{\vec {p}}/dt{\text{, where }}{\vec {p}}=m{\vec {v}}}$ is momentum. ▭ Impulse-momentum theorem ${\displaystyle {\vec {J}}=F_{ave}\Delta t=\int _{t_{i}}^{t_{f}}{\vec {F}}dt=\Delta {\vec {p}}}$. ▭ For 2 particles in 2D ${\displaystyle {\text{If }}{\vec {F}}_{ext}=0{\text{ then }}\sum _{j=1}^{N}{\vec {p}}_{j}=0\Rightarrow p_{f,\alpha }=p_{1,i,\alpha }+p_{2,i,\alpha }}$ where (α,β)=(x,y) ▭ Center of mass: ${\displaystyle {\vec {r}}_{CM}={\tfrac {1}{M}}\sum _{j=1}^{N}m_{j}{\vec {r}}_{j}\rightarrow {\tfrac {1}{M}}\int {\vec {r}}dm,}$ ${\displaystyle {\vec {v}}_{CM}={\tfrac {\,d}{dt}}{\vec {r}}_{CM}}$, and ${\displaystyle {\vec {p}}_{CM}=\sum _{j=1}^{N}m_{j}{\vec {v}}_{j}=M{\vec {v}}_{CM}.}$ ▭ ${\displaystyle {\vec {F}}={\tfrac {\,d}{dt}}{\vec {p}}_{CM}=m{\vec {a}}_{CM}=\sum _{j=1}^{N}m_{j}{\vec {a}}_{j}}$ ^[22] 10. Fixed-Axis_Rotation: 

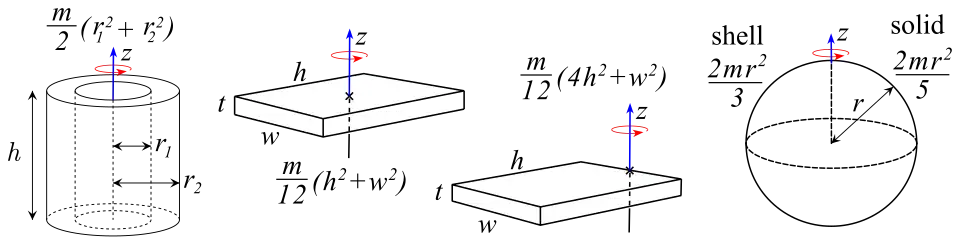
${\displaystyle \theta =s/r\,}$ is angle in radians,${\displaystyle \,\omega =d\theta /dt\,}$ is angular velocity; ▭ ${\displaystyle \,v_{t}=\omega r=ds/dt\,}$ is tangential speed. Angular acceleration is ${\displaystyle \alpha =d\omega /dt=d^{2}\theta /dt^{2}\,}$. ${\displaystyle a_{t}=\alpha r=d^{2}s/dt^{2}\,}$ is the tangential acceleration. ▭ Constant angular acceleration ${\displaystyle {\bar {\omega }}={\tfrac {1}{2}}(\omega _{0}+\omega _{f})\,}$ is average angular velocity. ▭ ${\displaystyle \theta _{f}=\theta _{0}+{\bar {\omega }}t=\theta _{0}+\omega _{0}t+{\tfrac {1}{2}}\alpha t^{2}\,.}$ ▭ ${\displaystyle \omega _{f}=\omega _{0}+\alpha t.\,}$ ${\displaystyle \omega _{f}^{2}=\omega _{0}^{2}+2\alpha \Delta \theta \,.}$ ▭ Total acceleration is centripetal plus tangential: ${\displaystyle {\vec {a}}={\vec {a}}_{c}+{\vec {a}}_{t}.\,}$ ▭ Rotational kinetic energy is ${\displaystyle K={\tfrac {1}{2}}I\omega ^{2},\,}$ where ${\displaystyle I=\sum _{j}m_{j}r_{j}^{2}\rightarrow \int r^{2}dm}$ is the Moment of inertia. ▭ parallel axis theorem ${\displaystyle I_{parallel-axis}=I_{center\,of\,mass}+md^{2}}$ ▭ Restricting ourselves to fixed axis rotation, ${\displaystyle r}$ is the distance from a fixed axis; the sum of torques, ${\displaystyle {\vec {\tau }}={\vec {r}}\times {\vec {F}}}$ requires only one component, summed as ${\displaystyle \tau _{net}=\sum \tau _{j}=\sum r_{\perp _{j}}F_{j}=I\alpha }$. ▭ Work done by a torque is ${\displaystyle dW=\left(\sum \tau _{j}\right)d\theta }$. The Work-energy theorem is ${\displaystyle K_{B}-K_{A}=W_{AB}=\int _{\theta _{A}}^{\theta _{B}}\left(\sum _{j}\tau _{j}\right)d\theta }$. ▭ Rotational power ${\displaystyle =P=\tau \omega }$. 11. Angular_Momentum:  Center of mass (rolling without slip) ${\displaystyle d_{CM}=r\theta ,\;}$ ${\displaystyle v_{CM}=r\omega ,\;}$${\displaystyle a_{MC}=R\alpha ={\tfrac {mg\sin \theta /}{m+\left(I_{cm}/r^{2}\right)}}}$ ▭ Total angular momentum and net torque: ${\displaystyle d{\vec {L}}/dt=\sum {\vec {\tau }}}$ ${\displaystyle ={\vec {l}}_{1}+{\vec {l}}_{2}+...;}$ ${\displaystyle {\vec {l}}={\vec {r}}\times {\vec {p}}\,}$ for a single particle. ${\displaystyle L_{total}=I\omega .}$ ▭ Precession of a top ${\displaystyle \omega _{P}=mrg/(I\omega ).}$ 12. Static_Equilibrium_and_Elasticity: Equilibrium ${\displaystyle \sum {\vec {F}}_{j}=0=\sum {\vec {\tau }}_{j}.\,}$ Stress = elastic modulus · strain (analogous to Force = k · Δ x ) ▭ (Young's , Bulk , Shear) modulus: ${\displaystyle \left({\tfrac {F_{\perp }}{A}}=Y\cdot {\tfrac {\Delta L}{L_{0}}}\,,\;\Delta p=B\cdot {\tfrac {-\Delta V}{V_{0}}}\,,\;{\tfrac {F_{\parallel }}{A}}=S\cdot {\tfrac {\Delta x}{L_{0}}}\right)}$ 13. Gravitation:  Newton's law of gravity ${\displaystyle {\vec {F}}_{12}=G{\tfrac {m_{1}m_{2}}{r^{2}}}{\hat {r}}_{12}}$ ▭ Earth's gravity ${\displaystyle g=G{\tfrac {M_{E}}{r^{2}}}}$ ▭ Gravitational PE beyond Earth ${\displaystyle U=-G{\tfrac {M_{E}m}{r}}}$ ▭ Energy conservation ${\displaystyle {\tfrac {1}{2}}mv_{1}^{2}-G{\tfrac {Mm}{r_{1}}}={\tfrac {1}{2}}mv_{2}^{2}-G{\tfrac {Mm}{r_{2}}}}$ ▭ Escape velocity ${\displaystyle v_{esc}={\sqrt {\tfrac {2GM_{E}}{r}}}}$ ▭ Orbital speed ${\displaystyle v_{orbit}={\sqrt {\tfrac {GM_{E}}{r}}}}$ ▭ Orbital period ${\displaystyle T=2\pi {\sqrt {\tfrac {r^{3}}{GM_{E}}}}}$ ▭ Energy in circular orbit ${\displaystyle E=K+U=-{\tfrac {GmM_{E}}{2r}}}$ ▭ Conic section ${\displaystyle {\tfrac {\alpha }{r}}=1+e\,\!\cos \theta }$ ▭ Kepler's third law${\displaystyle T^{2}={\tfrac {4\pi ^{2}}{GM}}a^{3}}$ ▭ Schwarzschild radius ${\displaystyle R_{S}={\tfrac {2GM}{c^{2}}}}$ 14. Fluid_Mechanics:  Mass density ${\displaystyle \rho =m/V\;}$ ▭ Pressure ${\displaystyle P=F/A\;}$ ▭ Pressure vs depth/height (constant density)${\displaystyle \,p=p_{o}+\rho gh\Leftarrow dp/dy=-\rho g}$ ▭ Absolute vs gauge pressure ${\displaystyle \,p_{abs}=p_{g}+p_{atm}\;}$ ▭ Pascal's principle: ${\displaystyle \,F/A\,}$ depends only on depth, not on orientation of A. ▭ Volume flow rate ${\displaystyle Q=dV/dt\;}$ ▭ Continuity equation ${\displaystyle \rho _{1}A_{1}v_{1}=\rho _{2}A_{2}v_{2}}$${\displaystyle \Rightarrow A_{1}v_{1}=A_{2}v_{2}{\text{ if }}\rho =const.\;}$ 15. Oscillations:  Frequency ${\displaystyle f}$, period ${\displaystyle T}$ and angular frequency ${\displaystyle \omega \,:\;}$ ${\displaystyle fT=1\,,\quad \omega T=2\pi }$ ▭ Simple harmonic motion ${\displaystyle x(t)=A\cos(\omega t+\phi ),\,}$ ${\displaystyle v(t)=-A\omega \sin(\omega t+\phi ),\,}$ ${\displaystyle a(t)=-A\omega ^{2}\cos(\omega t+\phi )}$ also models the x-component of uniform circular motion. ▭ For ${\displaystyle (A,\omega )}$ positive: ${\displaystyle \,x_{max}=A,\;v_{max}=A\omega ,\;a_{max}=A\omega ^{2}}$ ▭ Mass-spring ${\displaystyle \omega =2\pi /T=2\pi f={\sqrt {k/m}};\,}$ ▭ Energy ${\displaystyle E_{Tot}={\tfrac {1}{2}}kx^{2}+{\tfrac {1}{2}}mv^{2}={\tfrac {1}{2}}kA^{2}\Rightarrow }$${\displaystyle v=\pm {\sqrt {{\tfrac {k}{m}}\left(A^{2}-x^{2}\right)}}}$ ▭ Simple pendulum ${\displaystyle \omega \approx {\sqrt {g/L}}}$ ▭ Physical pendulum ${\displaystyle \tau =-MgL\sin \theta \approx -MgL\theta \Rightarrow \;}$${\displaystyle \omega ={\sqrt {mgL/I}}}$ and ${\displaystyle L}$ measures from pivot to CM. ▭ Torsional pendulum ${\displaystyle \tau =-\kappa \theta }$${\displaystyle \Rightarrow \omega ={\sqrt {I/\kappa }}}$ ▭ Damped harmonic oscillator ${\displaystyle m{\tfrac {d^{2}x}{dt^{2}}}=-kx-b{\tfrac {dx}{dt}}}$${\displaystyle \Rightarrow x=A_{0}e^{{\frac {b}{2m}}t}\cos {(\omega t+\phi )}}$ where ${\displaystyle \omega ={\sqrt {\omega _{0}^{2}-\left({\tfrac {b}{2m}}\right)^{2}}}}$ and ${\displaystyle \omega _{0}={\sqrt {\tfrac {k}{m}}}.}$ ▭ ^[23]Forced harmonic oscillator (MIT wiki!)] ${\displaystyle m{\tfrac {d^{2}x}{dt^{2}}}=-kx-b{\tfrac {dx}{dt}}+F_{0}\sin \omega t}$${\displaystyle \Rightarrow x=Ae^{{\frac {b}{2m}}t}\cos {(\omega t+\phi )}}$ where ${\displaystyle A={\tfrac {F_{0}}{\sqrt {m^{2}(\omega -\omega _{0})^{2}+b^{2}\omega ^{2}}}}}$. 16. Waves:  ^[24] Wave speed] (phase velocity) ${\displaystyle v=\lambda /T=\lambda f=\omega /k}$ where ${\displaystyle k=2\pi /\lambda }$ is wavenumber. ▭ Wave and pulse speed of a stretched string ${\displaystyle ={\sqrt {F_{T}/\mu }}}$ where ${\displaystyle F_{T}}$ is tension and ${\displaystyle \mu }$ is linear mass density. ▭ Speed of a compression wave in a fluid ${\displaystyle v={\sqrt {B/\rho }}.}$ ▭ Periodic travelling wave ${\displaystyle y(x,t)=A\sin(kx\mp \omega t)}$ travels in the positive/negative direction. The phase is ${\displaystyle kx\mp \omega t}$ and the amplitude is ${\displaystyle A}$. ▭ The resultant of two waves with identical amplitude and frequency ${\displaystyle y_{R}(x,t)=\left[2A\cos \left({\tfrac {\phi }{2}}\right)\right]\sin \left(kx-\omega t+{\tfrac {\phi }{2}}\right)}$ where ${\displaystyle \phi }$ is the phase shift. ▭ This wave equation ${\displaystyle \partial ^{2}y/\partial t^{2}=v_{w}^{2}\,\partial ^{2}y/\partial x^{2}}$ is linear in ${\displaystyle y=y(x,t)}$ ▭ Power in a tranverse stretched string wave ${\displaystyle P_{ave}={\tfrac {1}{2}}\mu A^{2}\omega ^{2}v}$. ▭ Intensity of a plane wave ${\displaystyle I=P/A\Rightarrow {\tfrac {P}{4\pi r^{2}}}}$ in a spherical wave. ▭ Standing wave ${\displaystyle y(x,t)=A\sin(kx)\cos(\omega t+\phi )}$ For symmetric boundary conditions ${\displaystyle \lambda _{n}=2\pi /k_{n}={\tfrac {2}{\pi }}L}$ ${\displaystyle n=1,2,3,...}$, or equivalently ${\displaystyle f=nf_{1}}$ where ${\displaystyle f_{1}={\tfrac {v}{2L}}}$ is the fundamental frequency. 17. Sound:  Pressure and displacement fluctuations in a sound wave ${\displaystyle P=\Delta P_{max}\sin(kx\mp \omega t+\phi )}$ and ${\displaystyle s=s_{max}\cos(kx\mp \omega t+\phi )}$ ▭ Speed of sound in a fluid ${\displaystyle v=f\lambda ={\sqrt {\beta /\rho }}}$, ▭ in a solid ${\displaystyle {\sqrt {Y/\rho }}}$, ▭ in an idal gas ${\displaystyle {\sqrt {\gamma RT/M}}}$, ▭ in air ${\displaystyle 331{\tfrac {m}{s}}{\sqrt {\tfrac {T_{K}}{273\,K}}}=331{\tfrac {m}{s}}{\sqrt {1+{\tfrac {T_{C}}{273^{o}C}}}}}$ ▭ Decreasing intensity spherical wave ${\displaystyle I_{2}=I_{1}\left({\tfrac {r_{1}}{r_{2}}}\right)^{2}}$ ▭ Sound intensity ${\displaystyle I={\tfrac {\langle P\rangle }{A}}={\tfrac {\left(\Delta P_{max}\right)^{2}}{2\rho v}}}$ ▭  ...level ${\displaystyle 10\log _{10}{I/I_{0}}}$ ▭ Resonance tube One end closed: ${\displaystyle \lambda _{n}={\tfrac {4}{n}}L,}$ ${\displaystyle f_{n}=n{\tfrac {v}{4L}},}$ ${\displaystyle n=1,3,5,...}$ ▭ Both ends open: ${\displaystyle \lambda _{n}={\tfrac {2}{n}}L,}$ ${\displaystyle f_{n}=n{\tfrac {v}{2L}},}$ ${\displaystyle n=1,2,3,...}$ ▭ Beat frequency ${\displaystyle f_{beat}=|f_{2}-f_{1}|}$ ▭ (nonrelativistic) Doppler effect ${\displaystyle f_{O}=f_{s}{\tfrac {v\pm v_{o}}{v\mp v_{s}}}}$ where ${\displaystyle v}$ is the speed of sound, ${\displaystyle v_{s}}$ is the velocity of the source, and ${\displaystyle v_{o}}$ is the velocity of the observer. ▭ Angle of shock wave ${\displaystyle \sin \theta =v/v_{s}=1/M}$ where ${\displaystyle v}$ is the speed of sound, ${\displaystyle v_{s}}$ is the speed of the source, and ${\displaystyle M}$ is the Mach number.

I=∫r²dm for a hoop, disk, cylinder, box, plate, rod, and spherical shell or solid can be found from this figure.