University of Florida/Egm4313/s12.team11.R1
Report 1
Intermediate Engineering Analysis
Section 7566
Team 11
Due date: February 1, 2012.
Problem R1.1: Spring-dashpot system
Solved by Francisco Arrieta
Problem Statement
- Derive the equation of motion of a spring-dashpot system in parallel, with a mass and applied force .
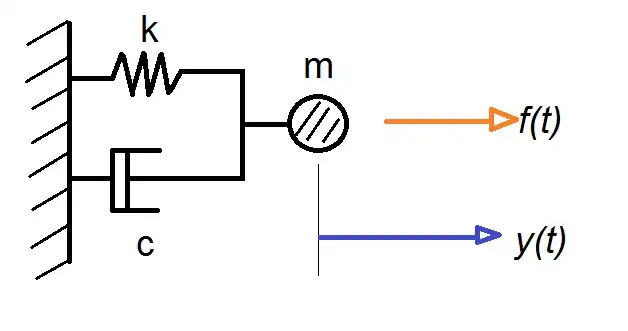
Solution
Kinematics
- (1)
- Since the spring and dashpot are placed parallel to each other, they will experience the same deformation when a force is applied on the system
Kinetics
- (2)
- Based on Newton's Second Law of Motion where is the second derivative of position with respect to time
Relations
- (3)
- (4)
Using (1) in (2)&(3):
Then (2) becomes:
Created by: Francisco Arrieta 22:05, 31 January 2012 (UTC)
Problem R1.2: Spring-mass-dashpot system (parallel)
Solved by Kyle Gooding
Problem Statement
Derive the equation of motion of the spring-mass-dashpot, with an applied force on the ball.
Figures
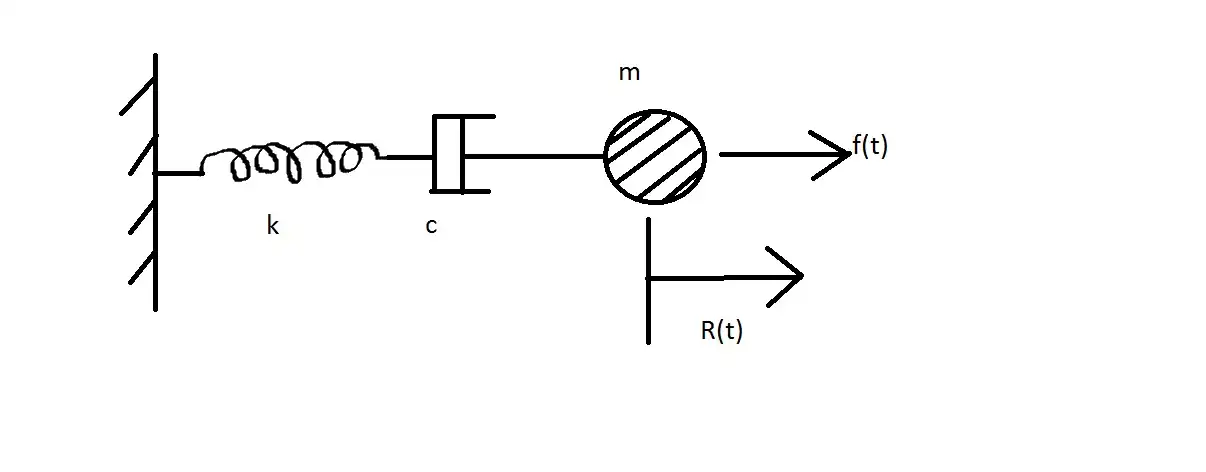
Solution
Kinematics
Kinetics
Spring
Dashpot
Mass
Forcing Function
Sum of Forces
Substitution
And finally we find:
Created By: Kyle Gooding 01:46, 29 January 2012 (UTC)
Problem R1.3: Spring-mass-dashpot system (series)
Solved by Luca Imponenti
Problem Statement
For the spring-dashpot-mass system shown, draw the FBDs and derive the following equation of motion
Figures
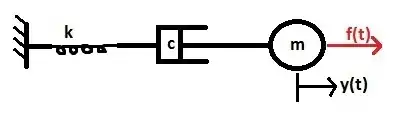
Free Body Diagram
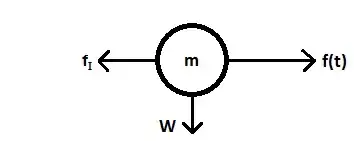
Solution
Where fI is the resistive force from both the spring and dash-pot and f(t) is our applied force.
Kinetics
which can be re-written as
Created by: Luca Imponenti 03:01, 30 January 2012 (UTC)
Problem R1.4: Circuit equation derivation
Solved by Gonzalo Perez
Problem Statement
Derive (3) and (4) from (2).
Given:
(2)
(3)
(4)
Solution
First, let's solve for (3).
Recall that:
,
and
.
We can use this information to replace the differentiating terms accordingly.
After doing so, we get:
but knowing that , we can rearrange the terms to get .
Using this information in the previously derived equation, we find that:
.
Finally, after differentiating with respect to , we get:
.
Now, let's solve for (4).
Once again considering that , we can solve for (4) by differentiating
twice and then plugging it into (2).
Deriving twice, we find that:
After plugging this into (2), we see that:
.
Once rearranging , we find that .
We can plug this in to the above equation to get the solution:
Created by: Gonzalo Perez 22:07, 31 January 2012 (UTC)
Problem R1.5: General solutions to ODEs
Solved by Jonathan Sheider
These problems are taken directly from Erwin Kreyszig's Advanced Engineering Mathematics, p.59 problems 4-5. The theory behind solving the differential equations is based on the derived mathematical approach to Solving Homogeneous Linear ODE's with Constant Coefficients (Erwin Kreyszig's Advanced Engineering Mathematics, pages 53-59).
K 2011 p.59 pb. 4
Problem Statement
Find a general solution to the given ODE. Check your answer by substituting into the original equation.
Given:
Solution
The characteristic equation of this ODE is therefore:
Evaluating the discriminant:
Therefore the equation has two complex conjugate roots and a general homogenous solution of the form:
[1]
Where:
And finally we find the general homogenous solution:
Checking:
We found that:
Differentiating to obtain and respectively:
Substituting these equations into the original ODE yields:
Therefore this solution is correct.
K 2011 p.59 pb. 5
Problem Statement
Find a general solution to the given ODE. Check your answer by substituting into the original equation.
Given:
Solution
The characteristic equation of this ODE is therefore:
Evaluating the discriminant:
Therefore the equation has a real double root and a general homogenous solution of the form:
[2]
And finally we find the general homogenous solution:
Checking:
We found that:
Differentiating to obtain and respectively:
And,
Substituting these equations into the original ODE yields:
Therefore this solution is correct.
Created by: Jonathan Sheider 16:27, 31 January 2012 (UTC)
Problem R1.6: ODE linearity and superposition
Solved by Daniel Suh
Problem Statement
For each Ordinary Differential Equations, determine the order, linearity, and show whether the principal of superposition can be applied.
Order of ODEs
To find the order of Ordinary Differential Equations, (ODEs) simply check the differential order of the dependent variable. If the dependent variable is differentiated once, then it is a first order ODE. If it is differentiated twice, it is a second order ODE.
Linearity
To find the linearity of the ODE, check the power of the dependent variable. If the dependent variable is raised to the power of anything one than 1, then it is not linear. If the dependent variable is raised to the power of 1, then it is linear.
Superposition Principle
For a homogeneous linear ODE (2), any linear combination of two solutions on an open interval I is again a solution of (2) on I. In particular, for such an equation, sums and constant multiples of solutions are again solutions.[3]
The function satisfies the superposition principle if the sum of the homogeneous solution and the particular solution is equal to , with
Solutions
R1.6a
- Check superposition principle:
Order of ODE: 2nd Order Linearity: Linear Superposition Principle: Yes
R1.6b
- Check superposition principle:
Order of ODE: 1st Order Linearity: Non-linear Superposition Principle: No
R1.6c
- Check superposition principle:
Order of ODE: 1st Order Linearity: Non-linear Superposition Principle: No
R1.6d
- Check superposition principle:
Order of ODE: 2nd Order Linearity: Linear Superposition Principle: Yes
R1.6e
- Check superposition principle:
Order of ODE: 2nd Order Linearity: Linear Superposition Principle: Yes
R1.6f
- Check superposition principle:
Order of ODE: 2nd Order Linearity: Linear Superposition Principle: Yes
R1.6g
- Check superposition principle:
Order of ODE: 4th Order Linearity: Linear Superposition Principle: Yes
R1.6h
- Check superposition principle:
Order of ODE: 2nd Order Linearity: Non-linear Superposition Principle: No
R1.6i
Order of ODE: 1st Order Linearity: Non-linear Superposition Principle: N/A
Created by [Daniel Suh] 21:59, 31 January 2012 (UTC)
References
Kreyszig, Erwin; Herbert Kreyszig, Edward J. Norminton (2011). Advanced Engineering Mathematics. John Wiley & Sons, Inc. ISBN 978-0-470-45836-5.
Table of contributions
| Name | Responsibilities | Link to lecture | Checked by | Signature |
|---|---|---|---|---|
| Francisco Arrieta | Problem R1.1 | Sec 1 (d) | Andrea Vargas | --[Andrea Vargas] 16:39, 1 February 2012 (UTC) |
| Kyle Gooding | Problem R1.2 | Sec 1 (d) | Andrea Vargas | --[Andrea Vargas] 16:39, 1 February 2012 (UTC) |
| Luca Imponenti | Problem R1.3 | Sec 1 (d) | Andrea Vargas | --[Andrea Vargas] 16:39, 1 February 2012 (UTC) |
| Gonzalo Perez | Problem R1.4 | Sec 2 (d) | Andrea Vargas | --[Andrea Vargas] 16:39, 1 February 2012 (UTC) |
| Jonathan Sheider | Problem R1.5 | Sec 2 (d) | Andrea Vargas | --[Andrea Vargas] 16:39, 1 February 2012 (UTC) |
| Daniel Suh | Problem R1.6 | Sec 2 (d) | Andrea Vargas | --[Andrea Vargas] 16:39, 1 February 2012 (UTC) |
| Andrea Vargas | Report typing and formatting | N/A | Team 11 | -- [Team 11] 16:57, 1 February 2012 (UTC) |