According to the authors of this paper, to improve the performance, they decided to
drop backward pass and using a first-order approximation
I found a blog which discussed how to derive the math but got stuck along the way (please refer to the embedded image below):
- Why
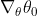 disappeared in the next line.
disappeared in the next line. - How come
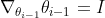 (which is an Identity matrix)
(which is an Identity matrix)
Update: I also found another math solution for this. To me it looks less intuitive but there's no confusion with the disappearance of as in the first solution.

